Sortiert
Das Insertion-Sort ist ein einfacher und intuitiver Sortieralgorithmus, der darauf abzielt, eine Liste oder ein Array von Elementen in aufsteigender oder absteigender Reihenfolge zu sortieren. Der Algorithmus ist besonders effizient für kleinere Datensätze oder bereits teilweise sortierte Datensätze.
Der Grundgedanke des Insertion-Sorts ist ähnlich dem Sortieren von Spielkarten in der Hand: Man nimmt ein Element aus der Liste und fügt es an der richtigen Stelle in die bereits sortierten Elemente ein.
Hier ist der grundlegende Ablauf des Insertion-Sort:
- Beginne mit dem zweiten Element in der Liste.
- Vergleiche dieses Element mit den vorherigen Elementen in der sortierten Sequenz.
- Verschiebe das Element so lange nach links, bis es an die richtige Position in der sortierten Sequenz gelangt.
- Wiederhole Schritte 2 und 3 für jedes verbleibende Element in der Liste
Verschiebe das Element so lange nach links, bis es an die richtige Position in der sortierten Sequenz gelangt.
Die Laufzeitkomplexität des Insertion-Sorts beträgt im Durchschnitt O(n^2), was ihn weniger effizient macht als einige andere fortschrittlichere Sortieralgorithmen. Trotzdem kann der Insertion-Sort in bestimmten Situationen, insbesondere wenn die Liste bereits teilweise sortiert ist oder wenn die Liste klein ist, recht effizient sein. 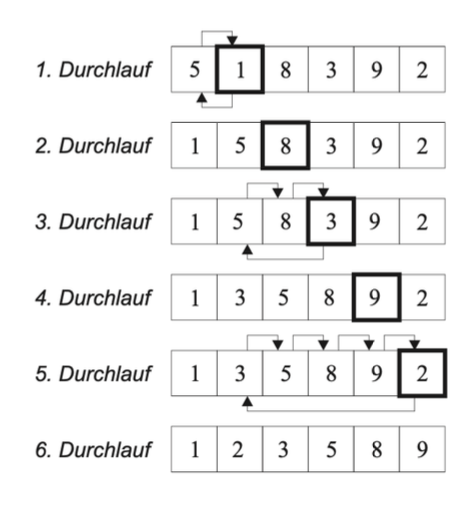
Hier ist eine einfache Implementierung des Insertion-Sorts in Java:
Insertion Sort
InsertionSort(array):
n = Länge des Arrays
für i von 1 bis i < n
key = array[i]
j = i - 1
solange j >= 0 und array[j] > key
array[j + 1] = array[j]
j = j - 1
array[j + 1] = key
public class InsertionSort {
public static void insertionSort(int[] array) {
int n = array.length;
int j = 0;
for (int i = 1; i < n; i++) {
int key = array[i];
j = i - 1;
while (j >= 0 && array[j] > key) {
array[j + 1] = array[j];
j--;
}
array[j + 1] = key;
}
}
public static void main(String[] args) {
int[] numbers = { 12, 8, 5, 14, 2 };
insertionSort(numbers);
System.out.println(Arrays.toString(numbers));
}
}
In diesem Beispiel wird die Methode insertionSort verwendet, um ein Array von Zahlen zu sortieren. Der Algorithmus durchläuft die Liste und fügt jedes Element in die richtige Position in der bereits sortierten Sequenz ein.
Selection Sort
Der Selection-Sort ist ein einfacher Sortieralgorithmus, der darauf abzielt, eine Liste oder ein Array von Elementen in aufsteigender oder absteigender Reihenfolge zu sortieren. Der Algorithmus arbeitet durch wiederholtes Auswählen des kleinsten (oder größten) Elements aus dem nicht sortierten Teil der Liste und tauscht es mit dem ersten Element im nicht sortierten Teil.
Der Selection-Sort arbeitet durch die folgenden Schritte:
- Suche das kleinste (oder größte) Element im nicht sortierten Teil der Liste.
- Tausche dieses Element mit dem ersten Element im nicht sortierten Teil.
- Vergrößere den sortierten Teil um eins, indem du das erste Element des nicht sortierten Teils in den sortierten Teil verschiebst.
- Wiederhole Schritte 1 bis 3, bis die gesamte Liste sortiert ist.
Die Laufzeitkomplexität des Selection-Sorts beträgt immer O(n^2), unabhängig von der Anordnung der Elemente. Dies macht ihn weniger effizient als andere fortschrittlichere Sortieralgorithmen, insbesondere für große Datensätze. Trotzdem ist der Selection-Sort aufgrund seiner einfachen Implementierung und seines intuitiven Ansatzes oft nützlich für kleine Datensätze oder als Lehrbeispiel für Sortieralgorithmen. 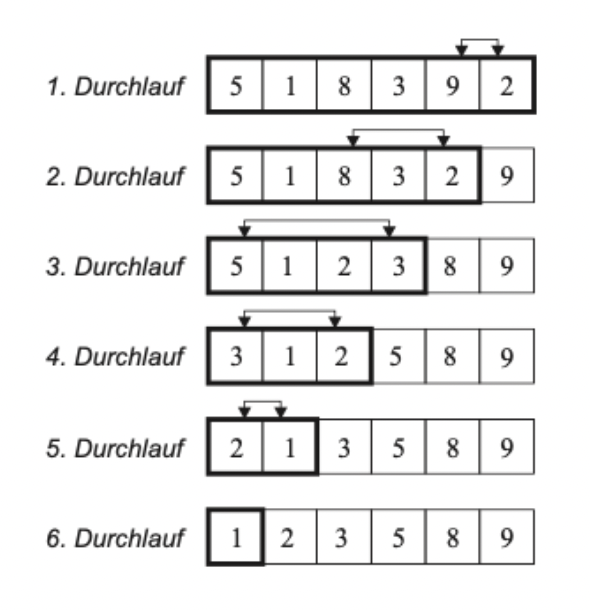
Hier ist eine einfache Implementierung des Selection-Sorts in Java:
//Pseudo Code
selectionSort(array arr)
n = length of arr
for i = 0 to i < n
minIndex = i
for j = i + 1 to n
if arr[j] < arr[minIndex]
minIndex = j
if minIndex ≠ i
swap arr[i] and arr[minIndex]
public class SelectionSort {
public static void selectionSort(int[] array) {
int n = array.length;
int temp = 0;
for (int i = 0; i < n ; i++) {
int minIndex = i;
for (int j = i + 1; j < n; j++) {
if (array[j] < array[minIndex]) {
minIndex = j;
}
}
temp = array[minIndex];
array[minIndex] = array[i];
array[i] = temp;
}
}
public static void main(String[] args) {
int[] numbers = { 12, 8, 5, 14, 2 };
selectionSort(numbers);
for (int num : numbers) {
System.out.print(num + " ");
}
}
}
In diesem Beispiel wird die Methode selectionSort verwendet, um ein Array von Zahlen zu sortieren. Der Algorithmus durchläuft die Liste und wählt in jedem Durchlauf das kleinste Element aus dem nicht sortierten Teil aus und tauscht es mit dem ersten Element im nicht sortierten Teil.
Bubble Sort
Bubble Sort ist ein einfacher Sortieralgorithmus, der darauf abzielt, eine Liste oder ein Array von Elementen in aufsteigender oder absteigender Reihenfolge zu sortieren. Der Name "Bubble Sort" stammt von der Art und Weise, wie die größten (oder kleinsten) Elemente allmählich "nach oben blubbern", wenn der Algorithmus durch die Liste geht.
Der Grundgedanke des Bubble Sort ist relativ einfach: Der Algorithmus vergleicht immer benachbarte Elemente und tauscht sie aus, wenn sie in der falschen Reihenfolge sind. Der größte (oder kleinste) Wert "blubbert" so allmählich an das Ende der Liste. Der Algorithmus wiederholt diesen Vorgang, bis die gesamte Liste sortiert ist. Der Bubble Sort arbeitet durch die folgenden Schritte:
- Durchlaufe die Liste von links nach rechts.
- Vergleiche jedes benachbarte Element.
- Wenn das rechte Element kleiner (oder größer) ist als das linke Element, tausche sie aus.
- Wiederhole Schritte 1 bis 3, bis keine Tausche mehr erforderlich sind.
Die Laufzeitkomplexität des Bubble Sort beträgt im Durchschnitt O(n^2), was ihn weniger effizient macht als andere Sortieralgorithmen wie Merge Sort oder Quick Sort. Aus diesem Grund wird Bubble Sort normalerweise für kleine Datensätze oder zu Lehrzwecken verwendet.
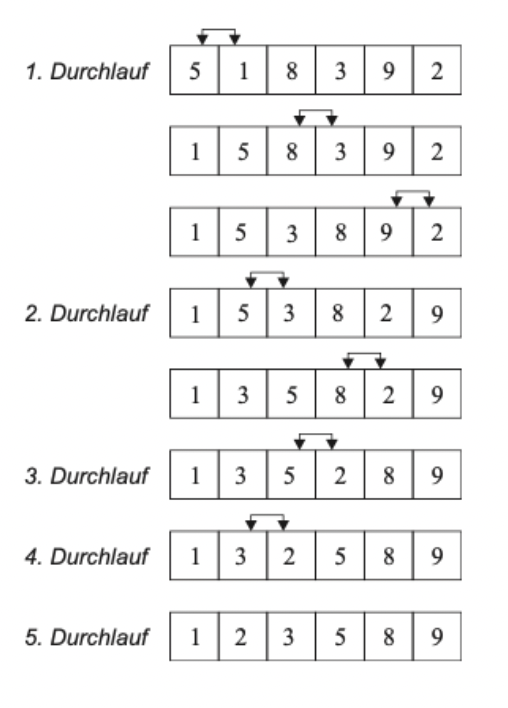
Hier ist eine einfache Implementierung des Bubble Sort in Java:
//Pseudo Code
bubbleSort(A: list of items)
n = length(A)
for i = 0 to i < n
for j = 0 to i < n - i - 1
if A[j] > A[j + 1]
swap(A[j], A[j + 1])
end if
end for
end for
end procedure
public class BubbleSort {
public static void bubbleSort(int[] array) {
int n = array.length;
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (array[j] > array[j + 1]) {
// Tausche die Elemente aus
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
}
}
}
}
public static void main(String[] args) {
int[] numbers = { 12, 8, 5, 14, 2 };
bubbleSort(numbers);
for (int num : numbers) {
System.out.print(num + " ");
}
}
}
Hier ist eine Implementierung des QuickSort-Algorithmus in Java:
public class QuickSort {
public static void quickSort(int[] array, int low, int high) {
if (low < high) {
int pivotIndex = partition(array, low, high);
quickSort(array, low, pivotIndex - 1);
quickSort(array, pivotIndex + 1, high);
}
}
public static int partition(int[] array, int low, int high) {
int pivot = array[high];
int i = low - 1;
for (int j = low; j < high; j++) {
if (array[j] < pivot) {
i++;
swap(array, i, j);
}
}
swap(array, i + 1, high);
return i + 1;
}
public static void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
public static void printArray(int[] array) {
for (int num : array) {
System.out.print(num + " ");
}
System.out.println();
}
public static void main(String[] args) {
int[] arr = {10, 7, 8, 9, 1, 5};
int n = arr.length;
System.out.println("Unsortiertes Array:");
printArray(arr);
quickSort(arr, 0, n - 1);
System.out.println("Sortiertes Array:");
printArray(arr);
}
}
Bubble Sort
In diesem Beispiel wird die Methode bubbleSort verwendet, um ein Array von Zahlen zu sortieren. Der Algorithmus durchläuft die Liste und tauscht benachbarte Elemente aus, wenn sie in der falschen Reihenfolge sind. Dieser Vorgang wird so oft wiederholt, bis die gesamte Liste sortiert ist.
Es gibt verschiedene Sortierverfahren, die jeweils unterschiedliche Vor- und Nachteile haben. Hier ist ein Vergleich einiger bekannter Sortieralgorithmen hinsichtlich ihrer Laufzeitkomplexität, Stabilität und Speicherbedarf:
Insertion Sort:
- Laufzeitkomplexität: O(n^2)
- Stabil: Ja
- Speicherbedarf: O(1)
- Beschreibung: Effizient für kleinere Datensätze oder bereits teilweise sortierte Daten.
Selection Sort:
- Laufzeitkomplexität: O(n^2)
- Stabil: Nein (kann stabil gemacht werden)
- Speicherbedarf: O(1)
- Beschreibung: Einfach zu implementieren, benötigt aber viele Vergleiche.
Bubble Sort:
- Laufzeitkomplexität: O(n^2)
- Stabil: Ja
- Speicherbedarf: O(1)
- Beschreibung: Einfach zu implementieren, jedoch ineffizient für große Datensätze.
Quick Sort:
- Laufzeitkomplexität: O(n log n) (durchschnittlich), O(n^2) (schlechtestes Szenario)
- Stabil: Nein
- Speicherbedarf: O(log n) (durchschnittlich)
- Beschreibung: Effizient, teilt die Liste basierend auf einem Pivot-Element auf.
Merge Sort:
- Laufzeitkomplexität: O(n log n)
- Stabil: Ja
- Speicherbedarf: O(n)
- Beschreibung: Effizient, teilt die Liste in kleinere Teillisten auf.
Heap Sort:
- Laufzeitkomplexität: O(n log n)
- Stabil: Nein
- Speicherbedarf: O(1)
- Beschreibung: Verwendet eine Datenstruktur namens Heap, effizient für große Datensätze.
Die Wahl des geeigneten Sortierverfahrens hängt von verschiedenen Faktoren ab, wie der Größe der Datenmenge, der Verteilung der Daten, der Stabilität und dem verfügbaren Speicher. In der Praxis verwenden moderne Programmiersprachen oft optimierte Sortieralgorithmen wie Timsort (eine Hybridversion von Merge Sort und Insertion Sort) oder Intro Sort (eine Kombination aus Quick Sort, Heap Sort und Insertion Sort) für eine bessere Leistung in unterschiedlichen Situationen.
Laufzeitkomplexität
- O(1) konstante Komplexität, die Laufzeit hängt nicht von der Datenmenge ab. z.B. Arrayzugriff, Hashtable
- O(n) lineare Komplexität, die Laufzeit ist proportional zur Datenmenge. z.B. Schleife über ein Array um einen Wert zu finden, Einlesen einer Treffermenge aus der Datenbank
- O(n2) quadratische Komplexität, eine doppelte Datenmenge vervierfacht die Laufzeit z.B. Bubble-Sort
- O(log n) logarithmische Komplexität, wird die Datenmenge jeweils verdoppelt, steigt die Laufzeit linear an z.B. Binäre Suche
- O(n log n) superlineare Komplexität, liegt zwischen (n) und (n2). Tritt zum Beispiel auf, wenn eine Schleife über eine Baumsuche gebildet wird. z.B. optimierte Sortieralgorithmen wie Quicksort
- O(2n) exponentielle Komplexität, die Laufzeit verdoppelt sich, wenn die Datenmenge um eine Einheit größer wird. z.B. Bilden aller Paare einer Menge, Türme von Hanoi als rekursiver Algorithmus
O(1)
int a = 5;
int[] array = {1, 2, 3, 4, 5};
int firstElement = array[0];
O(n)
for (int i = 1; i <= n; i++) {
sum += i;
}
O(n2)
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.println(array[i] + " " + array[j]);
}
}
Binäre Suche
O(log n)
while (low <= high) {
int mid = (low + high) / 2;
if (array[mid] == target) {
return mid;
} else if (array[mid] < target) {
low = mid + 1;
} else {
high = mid - 1;
}
}
O(n log n)
Quick Sort
O(2n)
int n = 5; // Beispielweise Eingabegröße
for (int i = 0; i < 2 * n; i++) {
System.out.println("Iteration " + i);
}
Aufgabe: Sortierverfahren vergleichen
Schreiben Sie ein Java-Programm, das verschiedene Sortieralgorithmen auf ein zufällig generiertes Array anwendet und die Laufzeiten der Algorithmen vergleicht.
- Erzeugen Sie ein zufälliges Array mit einer festgelegten Anzahl von Elementen.
- Implementieren Sie mindestens vier verschiedene Sortieralgorithmen, z.B. Insertion Sort, Selection Sort, Bubble Sort und Quick Sort.
- Wenden Sie die verschiedenen Sortieralgorithmen auf das zufällige Array an und messen Sie die Laufzeiten.
- Geben Sie die Laufzeiten der Algorithmen in der Konsole aus.
- Um die Zeit zu messen, nutzen Sie diese Funktion:
long startTime = System.nanoTime();
long endTime = System.nanoTime();
int diff = endTime - startTime;
Zusätzliche Herausforderung: Fügen Sie weitere Sortieralgorithmen hinzu, wie z.B. Merge Sort, und vergleichen Sie ihre Leistung.